머신러닝 회귀

선형회귀와 다항회귀를 알아보자

---

회귀(Regression)

• 수치 예측
• 해석이 매우 중요
• 데이터가 어떤 분포로 이루어져 있는가를 파악
• 가설검정 추론

머신러닝 관점에서의 회귀

• 수치 예측
• 오차(Error) == 실체 관축지 - 예측치
• 좋은 모델을 선정 == 오차가 적은 것

import numpy as np
import matplotlib.pyplot as plt

# 데이터 셋
# 농어 길이
perch_length = np.array(
    [8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 
     21.0, 21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 
     22.5, 22.7, 23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 
     27.3, 27.5, 27.5, 27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 
     36.5, 36.0, 37.0, 37.0, 39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 
     40.0, 42.0, 43.0, 43.0, 43.5, 44.0]
     )
# 농어 무게
perch_weight = np.array(
    [5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 
     110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 
     130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 
     197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 
     514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 
     820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 
     1000.0, 1000.0]
     )

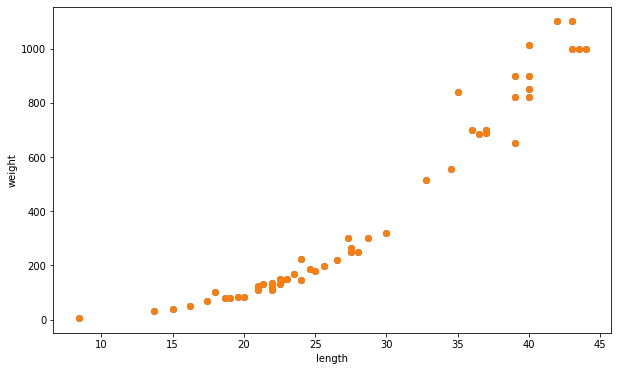
# 데이터 시각화
fig, ax = plt.subplots(figsize = (10,6))
ax.scatter(perch_length, perch_weight)
ax.scatter(perch_length, perch_weight)
ax.set_xlabel('length')
ax.set_ylabel('weight')

plt.show()

세트 분리 / 모델 예측

from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
import matplotlib.pyplot as plt

train_input, test_input, train_target, test_target = train_test_split(
    perch_length, perch_weight, random_state=42
)
knr = KNeighborsRegressor()

# K-최근접 이웃 회귀모델
# -> 근접한 이웃들을 근거로 하여 값을 예측
knr.fit(train_input, train_target)

# 파라미터 조정
knr.n_neighbors = 3

#모델 다시 훈련
knr.fit(train_input, train_target)

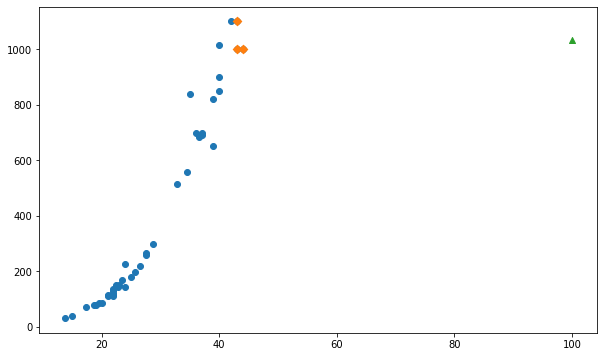
# 100cm 농어의 이웃을 구해보자
distances, indexes = knr.kneighbors([[100]])
print(knr.predict([[100]]))#결과 = [1033.33333]

fig, ax = plt.subplots(figsize=(10,6))
ax.scatter(train_input, train_target)
ax.scatter(train_input[indexes], train_target[indexes], marker = 'D')
#100cm 농어 데이터
ax.scatter(100,1033,marker='^')

plt.show()

---

선형회귀

• 길이가 100cm인 도미의 무게가 1kg?
• 예측 실패 -> 새로운 방법
• 직선을 긋는다
  • 주어진 데이터 분포에서 가장 작은 오차(군집도가 높은)를 표현할 수 있는 직선을 긋는다.

import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

lr = LinearRegression()

#선형 회귀 모델을 훈련
lr.fit(train_input, train_target)

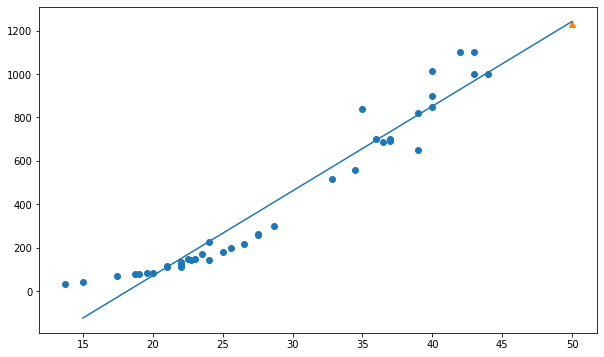
# 50cm농어 결과 = 1241.83860323
lr.predict([[50]])

fig, ax = plt.subplots(figsize=(10,6))
ax.scatter(train_input, train_target)

# 50cm 농어 데이터
ax.scatter(50,1231,marker='^')

# 기울기
                # x값 * 기울기 + 상수
ax.plot([15,50],[15 * lr.coef_ + lr.intercept_, 50 * lr.coef_ + lr.intercept_])

plt.show()

---

다항회귀

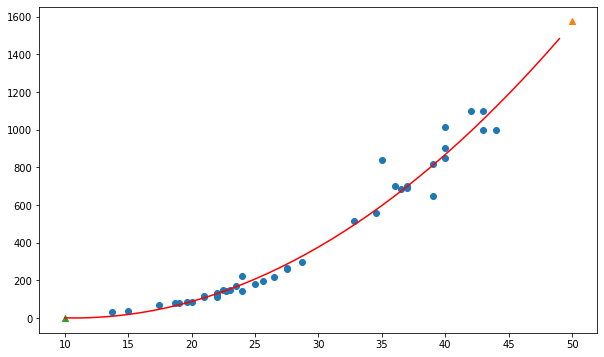
fig, ax = plt.subplots(figsize=(10,6))
point = np.arange(10,50)

# 훈련 세트의 산점도
ax.scatter(train_input, train_target)

# 2차 방정식 그래프
ax.plot(point, 1.01 * point ** 2 - 21.6 * point + 116.05, color='red')

ax.scatter(50,1574,marker='^')
ax.scatter(10,1.9,marker='^')

plt.show()